本文是学习笔记,只为通过讲述,在整理、归纳、总结材料的过程中,了解自己的不足。请凭自主思想预览,避免重复错误,被我带偏。
开关控制: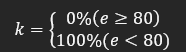 当检测值(e)<目标值 功率k=100%;当检测值(e)<目标值 功率k =0%
当检测值(e)<目标值 功率k=100%;当检测值(e)<目标值 功率k =0%
我们常见的控制模式是开关,打开开关,满功率运行;关闭开关,停止运行。但是这种控制方式无法做到精细控制,实际量(测量值)往往会再“目标值”上下徘徊。比如加热水,定温80℃,加热器进行加热,传感器检测水温,当温度加热到80℃时,关闭加热器。但此时加热器的余温肯定比80℃高,仍然会给水传递热量,使得水温上升。比如上升3℃,达到83℃,余热散去。水向周围环境散发的热量 开始大于吸收的热量,水温降低。当降低到80℃时,打开加热器,但是此时加热器需要升温,并且需要水吸收的热量大于散发的热量,水温才能开始上升,致使水温仍然会下降,比如到77℃时,水吸收的热量大于散发的热量,水温开始上升,等待水温上升80℃。如此循环。
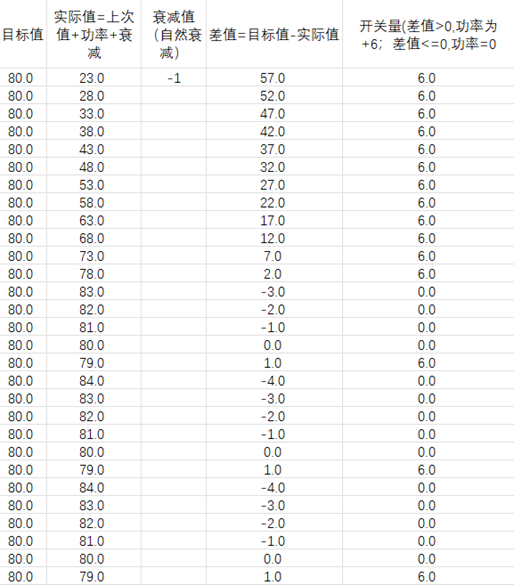
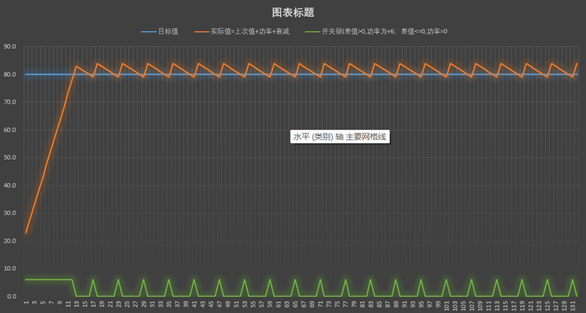
那么这种开关控制,带来的问题就会让水温在77℃~83℃之间徘徊。
问题1:如何消除这种徘徊的变化问题呢?
1、 将开关控制,变为比例控制(P)
u(t)=Kp*e(t)*100% e(t)为目标值与检测值的差值(偏差),当偏差e(t)较大时,u(t)=100%;当偏差e(t)较小时,u(t)= Kp*e(t)*100%
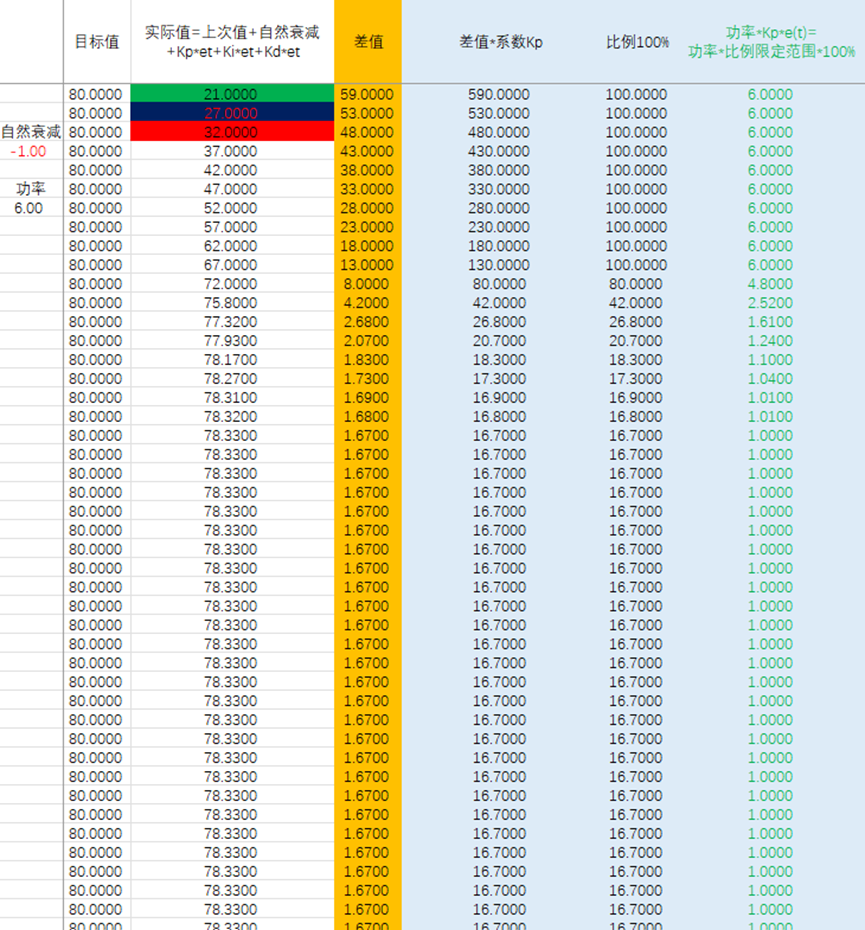
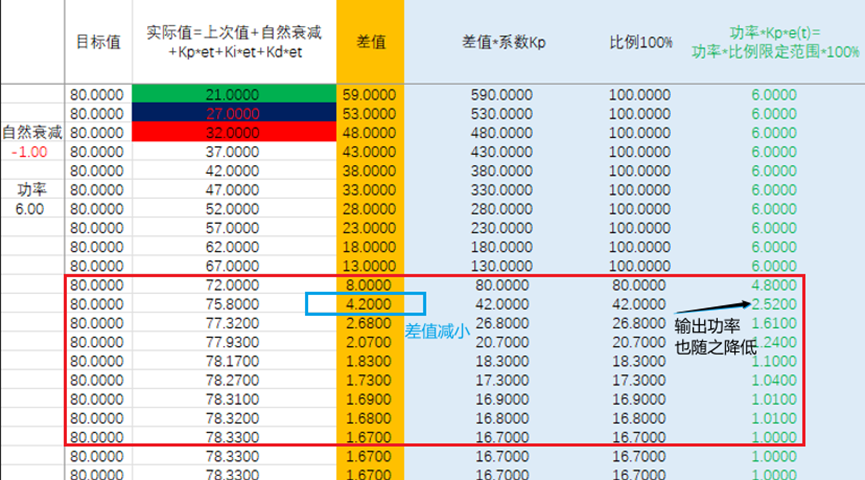
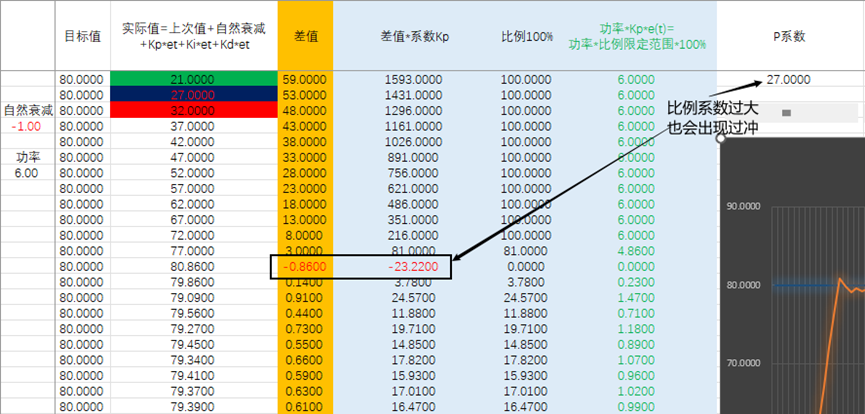
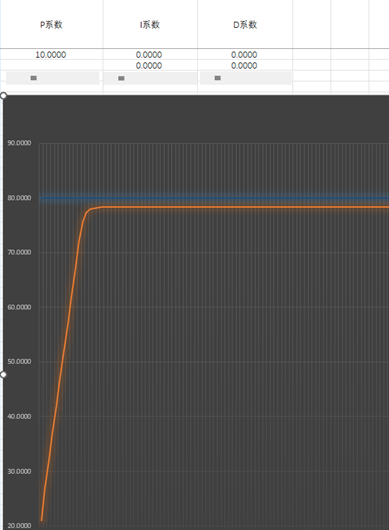
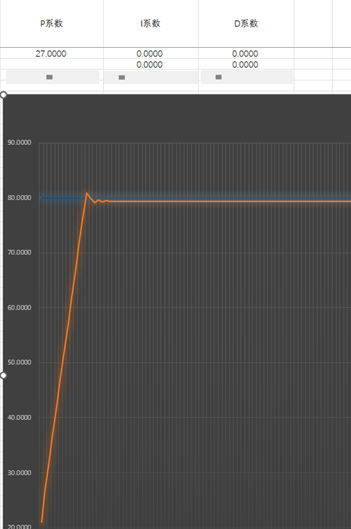
但是单纯比例系数调节,细心的会发现一个问题,就是无法达到目标值,差值总会存在。
问题2:如何消除最终稳定下来的差值呢?
2、引入积分量,将之前所有的差值进行累加,只要有差值存在,积分量就会不断变化(差值为正数,正向增加;差值为负数(检测值>目标值),积分值减小)
先看一下纯积分控制变化
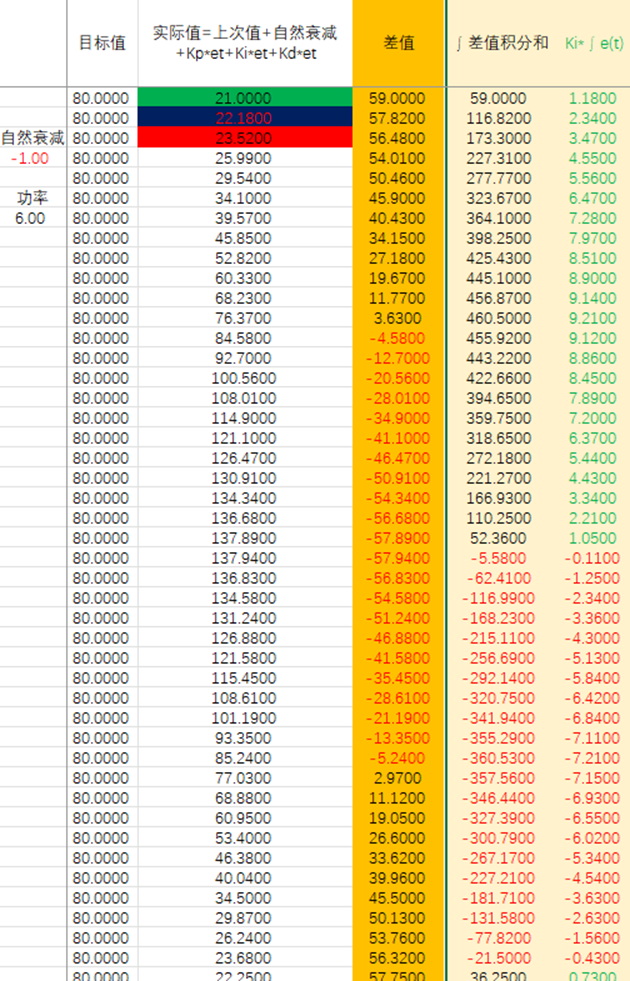
 积分变化是这个样子的,但是输出功率不可能无限输出,目前也没有用到反向输出,我们再限制一下功率输出
积分变化是这个样子的,但是输出功率不可能无限输出,目前也没有用到反向输出,我们再限制一下功率输出
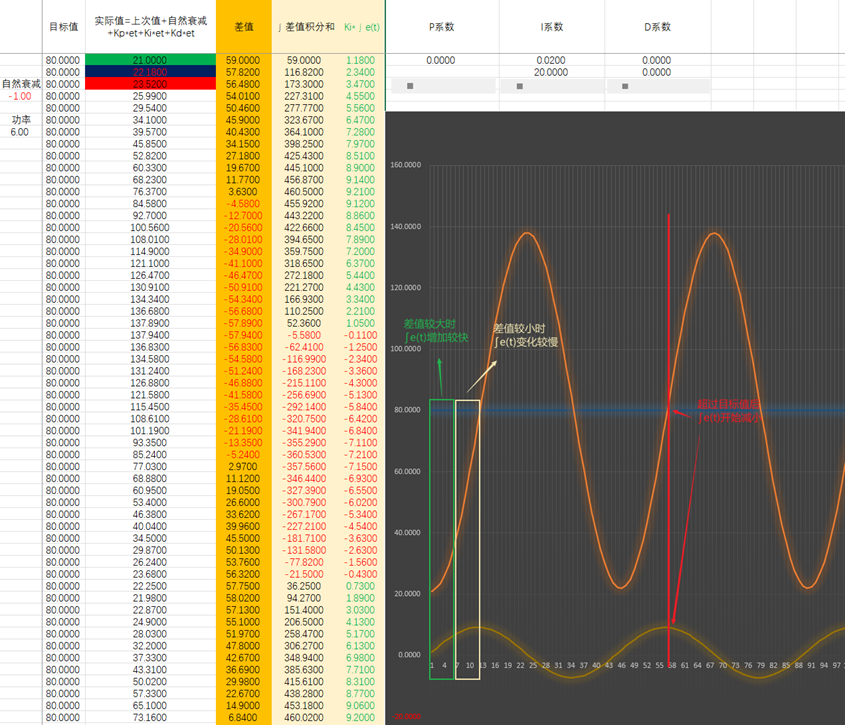
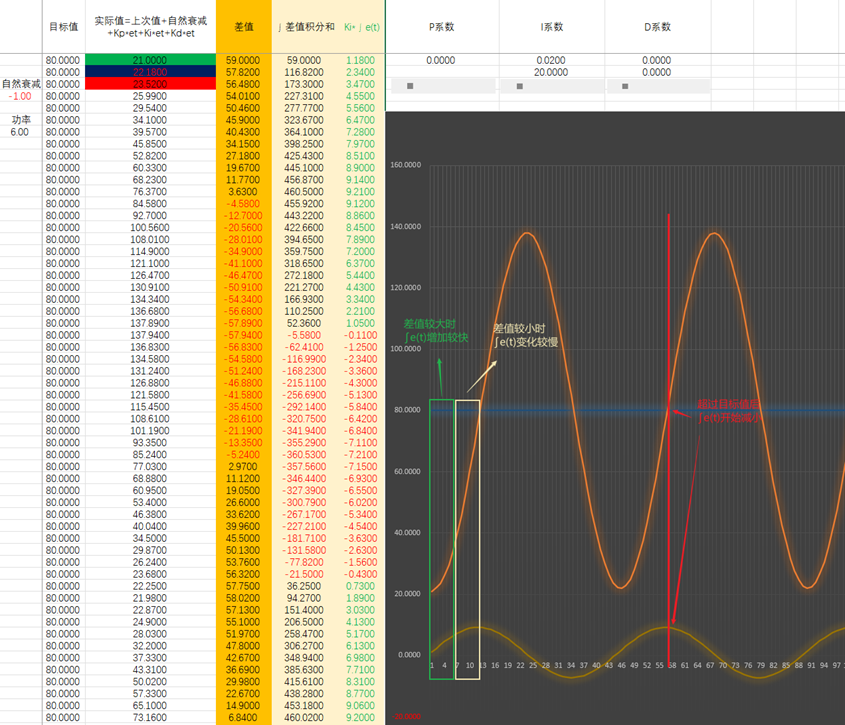
 我们在回到比例控制,将比例控制和积分控制进行叠加,我们来看一下效果
我们在回到比例控制,将比例控制和积分控制进行叠加,我们来看一下效果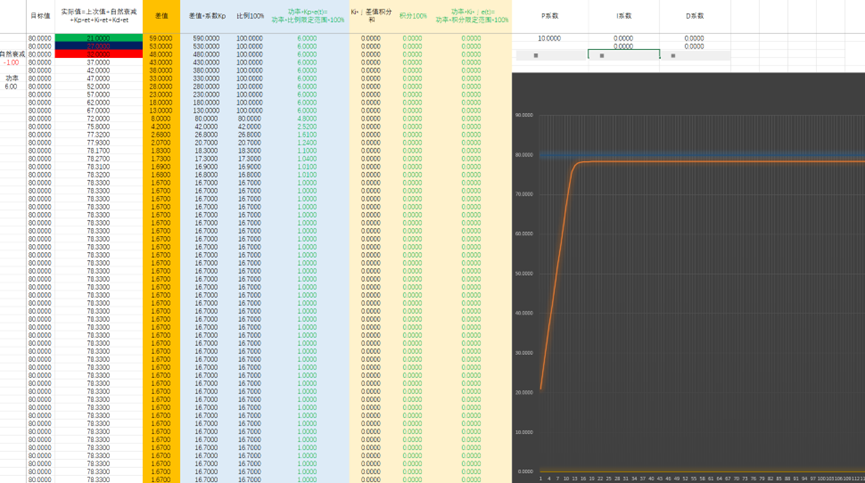
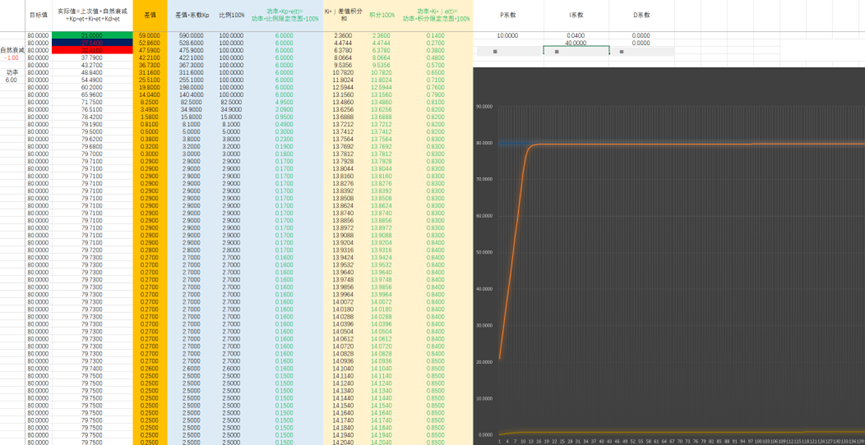
 我们继续增大Ki
我们继续增大Ki
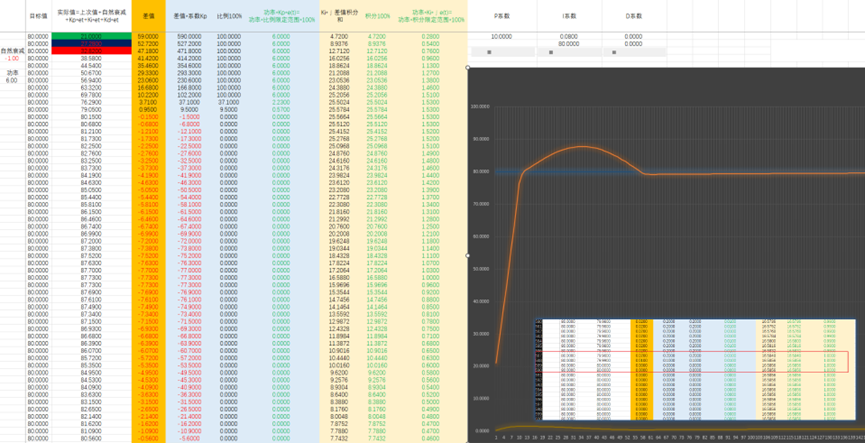
这是最快接近目标值的Ki
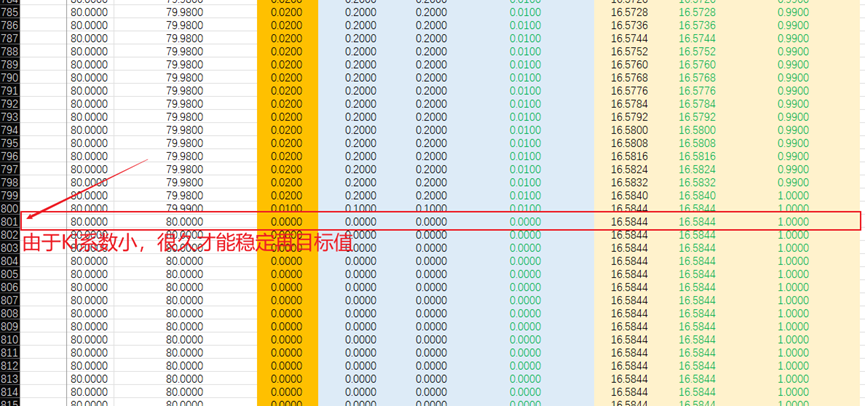
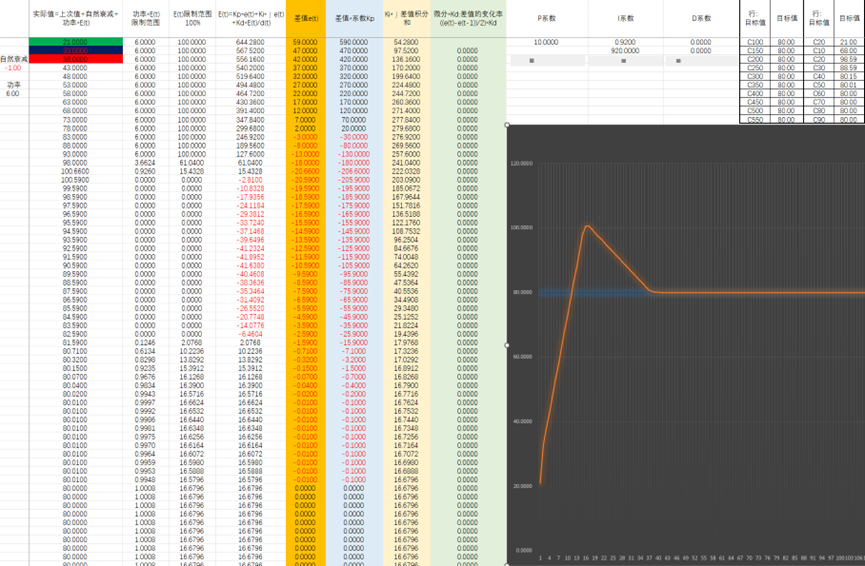
但是这仍然有问题,要么Ki值太小,仅仅是更接近目标值,想要达到并稳定在目标值需要很久很久;要么Ki值太大,能加快达到目标值,但会出现过冲的现象。
问题3:如何消除过冲呢?
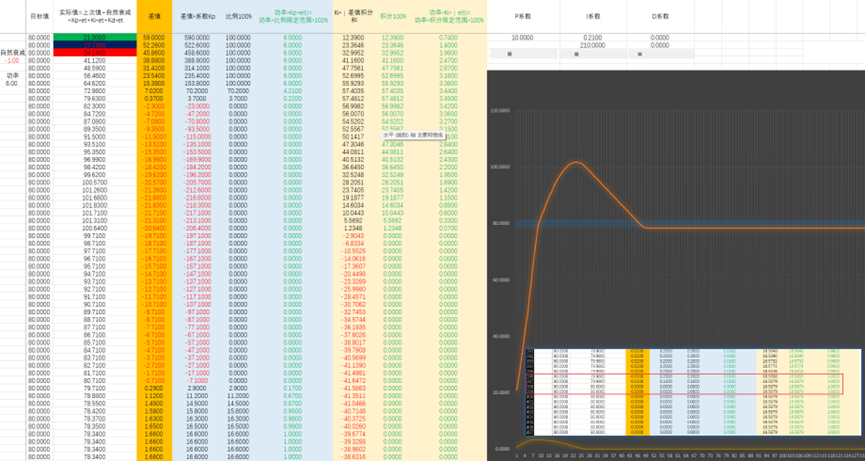
3、增加微分,即差值的变化速度,与整体变化进行抵消,变化越快,抵消值(微分值)就越大,进而阻止其快速变化。
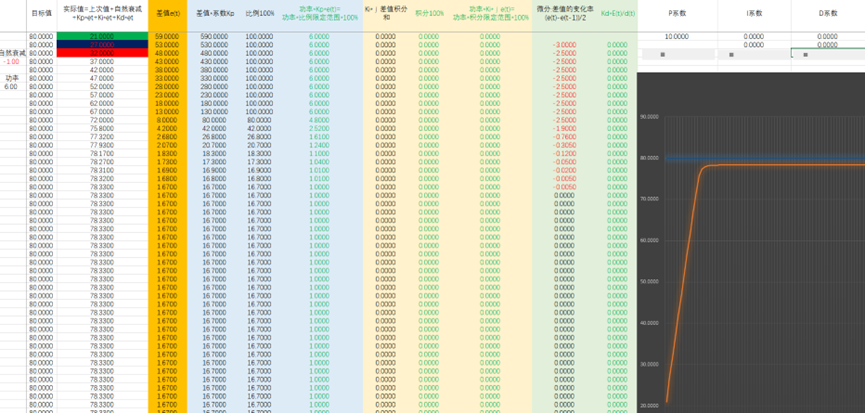
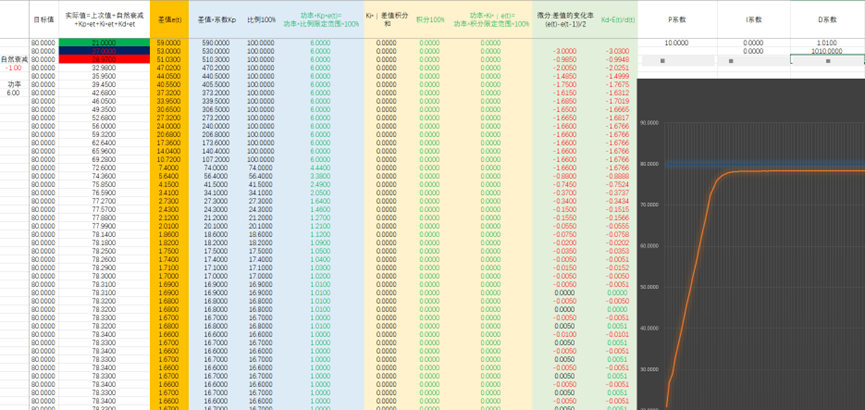
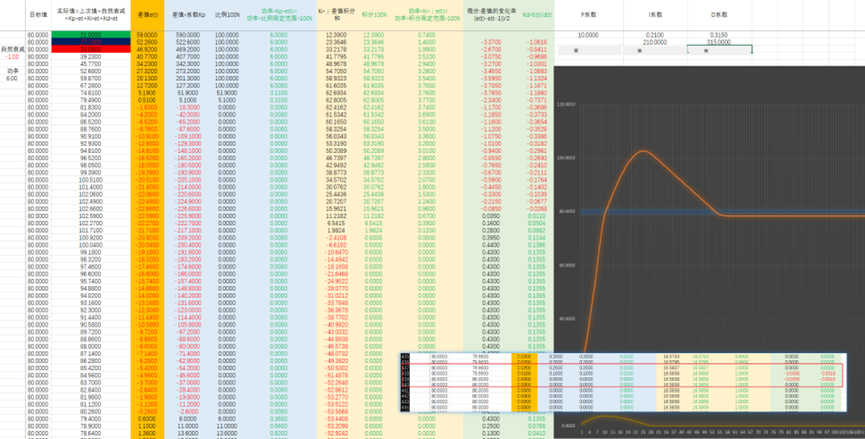
优美的中国话,翻车了,效果不好。改一下限制范围 PID系数计算关系,先计算E(t)=Kp*e(t)+Ki*∫e(t)+Kd*E(t)/d(t) 再限定E(t)范围,再乘以功率。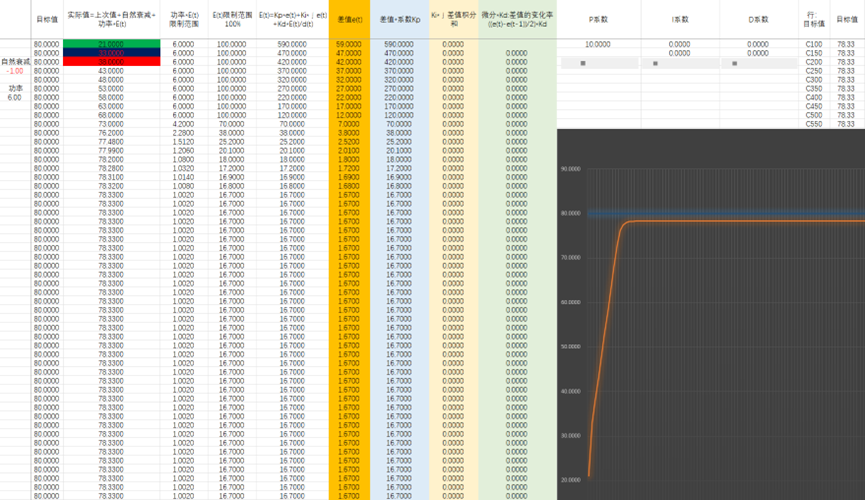
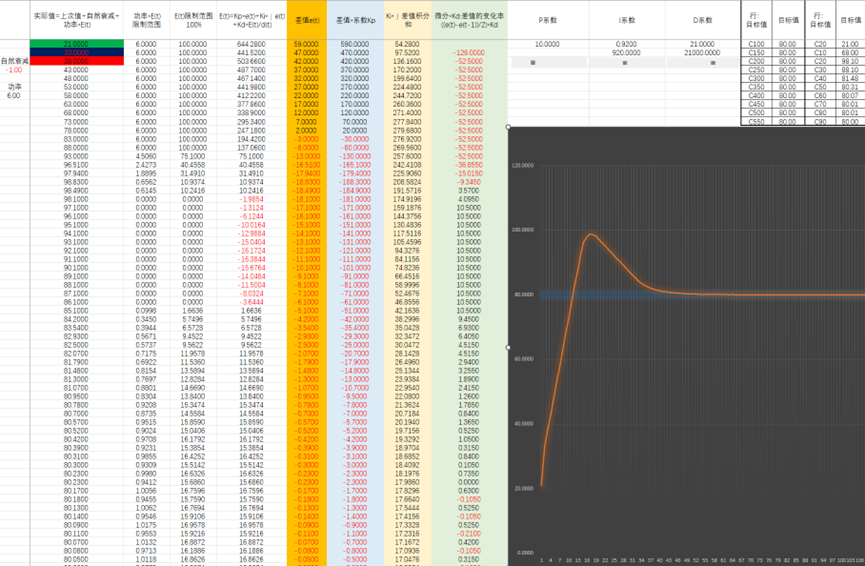
先这样吧,有时间再回顾,温故而知新。
